Embarking on a journey into the realm of geometry, we present the volume of prisms and cylinders worksheet answers, an invaluable resource meticulously crafted to empower learners with a comprehensive understanding of these fundamental shapes. Delving into the intricacies of volume calculations, this guide unveils the formulas, applications, and nuances that govern the measurement of three-dimensional objects.
Within these pages, we unravel the complexities of prism volume calculations, exploring the distinct characteristics of rectangular, triangular, and hexagonal prisms. Cylinders, too, take center stage as we delve into their volume formulas, uncovering the relationship between their radius and height.
A comparative analysis of prisms and cylinders ensues, highlighting their similarities and differences, while practical examples illustrate the significance of volume calculations in real-world contexts.
Volume of Prisms and Cylinders: Volume Of Prisms And Cylinders Worksheet Answers
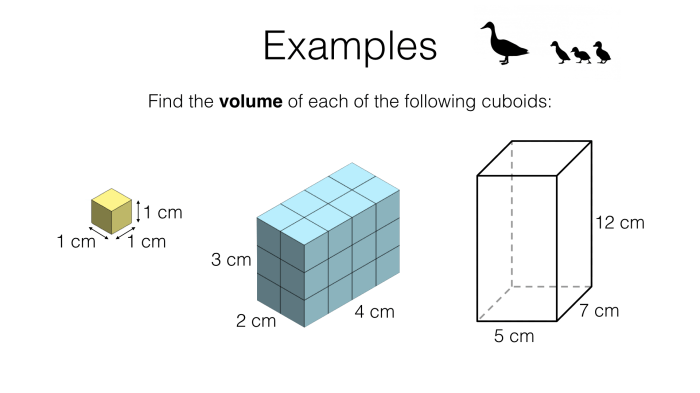
Volume is a measure of the amount of space occupied by a three-dimensional object. In geometry, prisms and cylinders are two common shapes for which we can calculate the volume.
1. Prism Volume Calculations
A prism is a polyhedron with two parallel faces called bases, which are congruent polygons. The other faces of the prism are parallelograms. The volume of a prism is calculated by multiplying the area of the base by the height of the prism.
- Formula: V = Bh, where V is the volume, B is the area of the base, and h is the height.
- Types of prisms:
- Rectangular prism
- Triangular prism
- Hexagonal prism
- Units of measurement: cubic units (e.g., cubic centimeters, cubic meters)
2. Cylinder Volume Calculations
A cylinder is a three-dimensional shape with two circular bases that are parallel and congruent. The height of the cylinder is the distance between the bases. The volume of a cylinder is calculated by multiplying the area of the base by the height of the cylinder.
- Formula: V = πr²h, where V is the volume, π is a mathematical constant approximately equal to 3.14, r is the radius of the base, and h is the height.
- Examples of real-world objects shaped like cylinders:
- Soda cans
- Pipes
- Barrels
- Relationship between radius and height: The volume of a cylinder is directly proportional to the square of the radius and the height.
3. Volume Comparison
Prisms vs. Cylinders

| Shape | Formula |
|---|---|
| Prism | V = Bh |
| Cylinder | V = πr²h |
Examples:
- To find the volume of a rectangular prism with a base area of 12 square centimeters and a height of 5 centimeters, we use the formula V = Bh = 12 cm² x 5 cm = 60 cubic centimeters.
- To find the volume of a cylinder with a radius of 3 centimeters and a height of 10 centimeters, we use the formula V = πr²h = 3.14 x 3² cm² x 10 cm = 282.6 cubic centimeters.
Similarities:
- Both prisms and cylinders have volume measured in cubic units.
- Both shapes have a base area and a height.
Differences:
- Prisms have polygonal bases, while cylinders have circular bases.
- The formula for calculating the volume of a cylinder includes the constant π, while the formula for a prism does not.
4. Applications of Volume Calculations
Volume calculations are used in various fields, including:
- Construction: Calculating the volume of concrete needed to pour a foundation or the volume of a building to determine its capacity.
- Engineering: Calculating the volume of a fuel tank or the volume of water flowing through a pipe.
- Manufacturing: Calculating the volume of a product to determine its weight or cost.
Accuracy in volume calculations is crucial because it ensures that the correct amount of material is used, the correct size of equipment is selected, and the product meets the desired specifications.
For irregular objects, such as rocks or sculptures, the volume can be estimated using methods like water displacement or 3D scanning.
Essential Questionnaire
What is the formula for calculating the volume of a prism?
Volume of prism = base area x height
How do I find the volume of a cylinder?
Volume of cylinder = πr²h
What are the units of measurement for volume?
Common units of volume include cubic centimeters (cm³), cubic meters (m³), and liters (L).